지난 시간에는 정방행렬 A가 주어지면 A의 역행렬을 구하는 알고리즘에 대해 배웠습니다. 이번에는 정방행렬 A를 두 개의 삼각행렬로 분해하는 LU Factorization 알고리즘에 대해 배워보겠습니다. 우선 LU Factorization에 대해 배우기 위해서는 삼각행렬이 뭔지 알아야겠죠? 삼각행렬(Triangular Matrix) 삼각행렬은 행렬의 원소 가운데 대각 원소 위(또는 아래)의 원소가 모두 0인 행렬을 의미합니다.예를 들면 아래와 같은 두 행렬은 모두 삼각행렬입니다. 이 중에서 0이 아닌 원소들이 위쪽에 존재하는 A의 경우 Upper Triangular Matrix라고 부르고, 아래쪽에 존재하는 B의 경우 Lower Triangular Matrix라고 부릅니다. Upper Triangular ..

지난 포스팅에서 단위행렬, 소거행렬, 역행렬, 치환행렬, 증강행렬에 대해서 배웠습니다. 이 용어들은 앞으로도 꾸준히 사용하게 될 용어입니다. 반드시 각 행렬들이 무엇을 의미하는지 알고 계시는 것을 권장드립니다. 이번 포스팅에서는 지난번에 소개해드린 행렬 중에 역행렬에 대해서 자세히 다루어볼까 합니다. 이차 정방행렬(2 by 2 Matrix)의 역행렬 지금은 사라졌다고 하지만 불과 몇 년 전까지만 해도 고등학교 교육과정상에는 행렬 단원이 존재했었습니다. 그리고 2차 정방행렬의 역행렬은 아래와 같다고 외웠었지요. 그러나 왜 2차 정방행렬의 역행렬이 저렇게 나오는지에 대해서는 배우지 않았을껍니다. (물론 A와 A의 역행렬의 곱이 Identity Matrix가 된다는 것은 쉽게 증명할 수 있지만요. 계산해보면 ..

선형대수학 시리즈 연재의 목차 초안입니다.해당 목차는 포스팅 상황에 따라 조금씩 변동될 수 있으며, 연재가 마치면 최종 목차를 다시 한번 포스팅하도록 하겠습니다. 선형대수학 시리즈는 총 25개의 포스팅으로 이루어질 예정입니다.포스팅 제목 뒤 괄호는 서적 의 단원을 의미합니다. 선형대수학과 직접적인 관련이 없는 일부 단원(6.3과 7단원 이후 단원)의 경우 연재에서 제외하였으며, 이는 추후 다른 연재 시리즈에서 다루도록 하겠습니다. [0] 선형대수학의 이해[1] 벡터, 연산 그리고 차원 (1.1, 1.2, 2.1)[2] 연립 선형 방정식 (2.1)[3] 소거법의 소개 (2.2)[4] 단위행렬, 소거행렬, 역행렬, 치환행렬, 증강행렬 (2.3, 2..

지난 강의에서는 소거법에 대해 간단하게 살펴보았습니다.지난 시간에 소거법에 대해 다루고 나서, 행렬을 이용한 소거법(소거행렬)까지 다루려고 하였으나, 그러기 위해서는 단위행렬(Identity Matrix)에 대한 설명이 필요해서 소거법의 개념만을 설명하는 짧은 포스팅으로 대체했었습니다. 이번 시간에는 단위행렬(Identity Matrix)과 소거행렬(Elimination Matrix)을 중점적으로 배우고, 역행렬(Inverse Matrix)과 치환행렬(Permutation Matrix), 증강행렬(Augmented Matrix)에 대해 정의해보도록 하겠습니다. 단위행렬(Identity Matrix)이란? 단위행렬은 행렬의 대각 원소(Diagonal Component)는 모두 1, 대각 원소가 아닌 원소들..

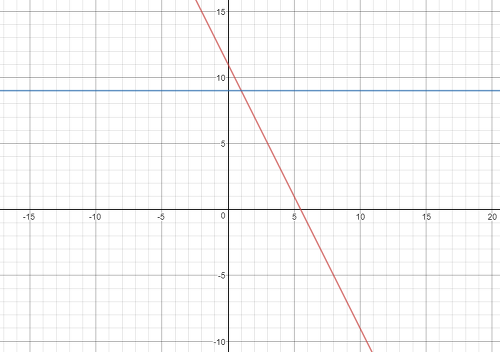
지난 포스팅에서는 연립 선형 방정식을 다루어 보았습니다.연립 방정식을 풀기 위해 Row Picture상에도 나타내 보았고, Column Picture 상에도 나타내 보았습니다. 또, 잠깐 스쳐서 설명하긴 했지만, 한 식에서 다른 한 식을 빼서, 하나의 미지수를 제거하는 방법도 소개했었지요. 이번 포스팅에서는 미지수를 제거해 나가면서 연립 방정식을 푸는 소거법(Elimination)에 대해 알아보겠습니다. 소거법과 Row Picture 지난시간에 다루었던 연립 일차 방정식을 다시 가져와볼까요? 지난 시간에 위의 식의 양 변에 4를 곱한 다음 아래 식을 빼서 이런 식을 도출해 낸 것을 기억하실껍니다. 따라서, 결국 최종적인 연립방정식은 아래와 같이 변하게 되었습니다. 그러면 Row Picture 상에 나타낸..

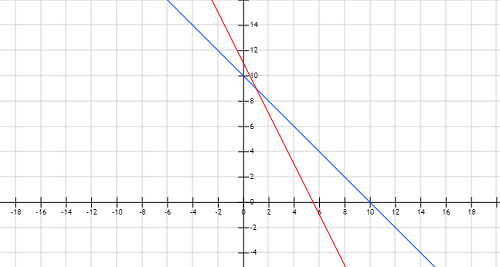
지난시간에는 벡터에 대한 기본 개념과 연산 방법에 대해 배워보았습니다. 그리고, 책에 나와있는 내용은 아니지만 선형대수학을 앞으로 배움에 있어서 꼭 필요한 내용인 "차원"에 대한 내용도 추가적으로 설명드렸습니다. 이번 포스팅에서는 여러개의 선형 방정식을 동시에 다루어 보도록 하겠습니다. 기초적인 내용이다 보니 내용이 길지 않고 쉬워보일 수 있지만, 마지막에 설명드리게 될 Row picture와 Column picture에 대한 내용은 중요한 개념이니 꼭 짚고 넘어가시길 바랍니다. 연립 선형 방정식 앞선 포스팅에서 말씀드렸듯, 우리는 이 연재과정을 다루는 동안 일차방정식만을 사용하겠다고 말씀드렸습니다. 다시 말해서 우리가 이번 포스팅에서 다루게 될 연립 선형 방정식 이라는 것은, 중학교 시절 배웠던 연립 ..

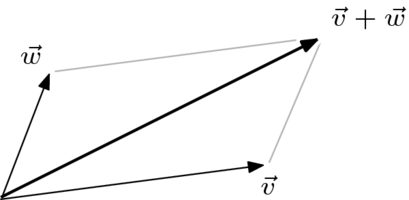
지난 포스팅에서 선형대수학의 기본 개념과 선형성의 정의에 대해 말씀드렸습니다.이번 포스팅에서는 벡터를 주로 다루어 보겠습니다. 벡터(Vector)란? 고등학교 교육과정을 거치신 분이라면 벡터가 무엇인지는 쉽게 정의하실 수 있으실 것이라 생각합니다.벡터는 크기만을 가지는 스칼라와 달리 크기와 방향을 모두 가지는 양입니다. 예를 들어서, 몸무게의 경우 70kg와 같이 크기만으로 나타낼 수 있지만위치의 경우 "원점에서부터 동쪽으로 40m" 처럼 크기와 방향 성분이 모두 필요합니다. 선형대수학에서는 백터를 아래와 같이 표현합니다. a와 b는 벡터의 성분(component)라고 불리며, v는 벡터라고 불립니다.특히 이 벡터는 행렬의 열(column)을 통해 표현되어지기 때문에 열벡터(Column Vector)라고..

앞으로 꾸준히 선형대수학에 대한 내용을 포스팅하고자 합니다.사실 오래 전에도 이러한 시리즈 포스팅을 시도해 본 적이 있지만 번번히 제 게으름을 이기지 못하고 포기해 왔었습니다. 제 게으름을 이기기 위해서는 구독해주시는, 혹은 지나가다가 우연히 이 연재를 본 독자분들의 관심이 필요합니다. 따뜻한 칭찬의 댓글도 좋고, 따끔한 비판 혹은 지적의 댓글도 모두 감사합니다. 이번에는 부디 마무리를 볼 수 있는 연재가 되기를 바라며 선형대수학 포스팅을 시작합니다. 먼저, 본 연재 시리즈는 아래와 같은 책을 기반으로 쓰여졌음을 밝힙니다. http://book.daum.net/detail/book.do?bookid=BOK00029578281AL=[ Introduction to Linear Algebra ] 이 포스팅을 ..